• Temporal Difference Learning and TD-Gammon
  • Complexity in the Game of Backgammon
  • TD-Gammon's Learning Methodology -- Figure 1.
  • Results of Training -- Table 1, Figure 2, Table 2, Figure 3, Table 3.
  • Understanding the Learning Process
    • Absolute Accuracy vs. Relative Accuracy
    • Stochastic Environment
    • Learning Linear Concepts First
  • Conclusion
• Appendix: Performance Measures
• Acknowledgments
• References
• About the Author

By Gerald Tesauro

Ever since the days of Shannon's proposal for a chess-playing algorithm [12] and Samuel's checkers-learning program [10] the domain of complex board games such as Go, chess, checkers, Othello, and backgammon has been widely regarded as an ideal testing ground for exploring a variety of concepts and approaches in artificial intelligence and machine learning. Such board games offer the challenge of tremendous complexity and sophistication required to play at expert level. At the same time, the problem inputs and performance measures are clear-cut and well defined, and the game environment is readily automated in that it is easy to simulate the board, the rules of legal play, and the rules regarding when the game is over and determining the outcome.

This article presents a game-learning program called TD-Gammon. TD-Gammon is a neural network that trains itself to be an evaluation function for the game of backgammon by playing against itself and learning from the outcome. Although TD-Gammon has greatly surpassed all previous computer programs in its ability to play backgammon, that was not why it was developed. Rather, its purpose was to explore some exciting new ideas and approaches to traditional problems in the field of reinforcement learning.

The basic paradigm of reinforcement learning is as follows: The learning agent observes an input state or input pattern, it produces an output signal (most commonly thought of as an "action" or "control signal"), and then it receives a scalar "reward" or "reinforcement" feedback signal from the environment indicating how good or bad its output was. The goal of learning is to generate the optimal actions leading to maximal reward. In many cases the reward is also delayed (i.e., is given at the end of a long sequence of inputs and outputs). In this case the learner has to solve what is known as the "temporal credit assignment" problem (i.e., it must figure out how to apportion credit and blame to each of the various inputs and outputs leading to the ultimate final reward signal).

The reinforcement learning paradigm has held great intuitive appeal and has attracted considerable interest for many years because of the notion of the learner being able to learn on its own, without the aid of an intelligent "teacher," from its own experience at attempting to perform a task. In contrast, in the more commonly employed paradigm of supervised learning, a "teacher signal" is required that explicitly tells the learner what the currect output is for every input pattern.

Unfortunately, despite the considerable attention that has been devoted to reinforcement learning over many years, so far there have been few practical successes in terms of solving large-scale, complex real-world problems. One problem has been that, in the case of reinforcement learning with delay, the temporal credit assignment aspect of the problem has remained extremely difficult. Another problem with many of the traditional approaches to reinforcement learning is that they have been limited to learning either lookup tables or linear evaluation functions, neither of which seem adequate for handling many classes of real-world problems.

However, in recent years there have been two major developments which have held out the prospect of overcoming these traditional limitations to reinforcement learning. One of these is the development of a wide variety of novel nonlinear function approximation schemes, such as decision trees, localized basis functions, spline-fitting schemes and multilayer perceptrons, which appear to be capable of learning complex nonlinear functions of their inputs.

The second development is a class of methods for approaching the temporal credit assignment problem which have been termed by Sutton "Temporal Difference" (or simply TD) learning methods. The basic idea of TD methods is that the learning is based on the difference between temporally successive predictions. In other words, the goal of learning is to make the learner's current prediction for the current input pattern more closely match the next prediction at the next time step. The most recent of these TD methods is an algorithm proposed in [13] for training multilayer neural networks called TD(lambda). The precise mathematical form of the algorithm will be discussed later. However, at this point it is worth noting two basic conceptual features of TD(lambda). First, as with any TD method, there is a heuristic error signal defined at every time step, based on the difference between two successive predictions, that drives the learning. Second, given that a prediction error has been detected at a given time step, there is an exponentially decaying feedback of the error in time, so that previous estimates for previous states are also corrected. The time scale of the exponential decay is governed by the lambda parameter.

TD-Gammon was designed as a way to explore the capability of multilayer neural networks trained by TD(lambda) to learn complex nonlinear functions. It was also designed to provide a detailed comparison of the TD learning approach with the alternative approach of supervised training on a corpus of expert-labeled exemplars. The latter methodology was used a few years ago in the development of Neurogammon, the author's previous neural-network backgammon program. Neurogammon was trained by backpropagation on a data base of recorded expert games. Its input representation included both the raw board information (number of checkers at each location), as well as a few hand-crafted "features" that encoded important expert concepts. Neurogammon achieved a strong intermediate level of play, which enabled it to win in convincing style the backgammon championship at the 1989 International Computer Olympiad [14]. Thus by comparing TD-Gammon with Neurogammon, one can get a sense of the potential of TD learning relative to the more established approach of supervised learning.

Before discussing the TD backgammon learning system, a few salient details regarding the game itself should be stated. Backgammon is an ancient two-player game (at least a thousand years older than chess, according to some estimates) that is played on an effectively one-dimensional track. The players take turns rolling dice and moving their checkers in opposite directions along the track as allowed by the dice roll. The first player to move all his checkers all the way forward and off his end of the board is the winner. In addition, the player wins double the normal stake if the opponent has not taken any checkers off; this is called winning a "gammon." It is also possible to win a triple-stake "backgammon" if the opponent has not taken any checkers off and has checkers in the farmost quadrant; however, this rarely occurs in practice.

The one-dimensional racing nature of the game is made considerably more complex by two additional factors. First, it is possible to land on, or "hit," a single opponent checker (called a "blot") and send it all the way back to the far end of the board. The blot must then re-enter the board before other checkers can be moved. Second, it is possible to form blocking structures that impede the forward progress of the opponent checkers. These two additional ingredients lead to a number of subtle and complex expert strategies [7].

Additional complexity is introduced through the use of a "doubling cube" through which either player can offer to double the stakes of the game. If the opponent accepts the double, he gets the exclusive right to make the next double, while if he declines, he forfeits the current stake. Hence, the total number of points won at the end of a game is given by the current value of the doubling cube multiplied by 1 for a regular win (or for a declined double), 2 for a gammon, and 3 for a backgammon.

Strategy for use of the doubling cube was not included in TD-Gammon's training. Instead, a doubling algorithm was added after training that makes decisions by feeding TD-Gammon's expected reward estimates into a theoretical doubling formula developed in the 1970s [16].

Programming a computer to play high-level backgammon has been found to be a rather difficult undertaking. In certain simplified endgame situations, it is possible to design a program that plays perfectly via table look-up. However, such an approach is not feasible for the full game, due to the enormous number of possible states (estimated at over 10 to the power of 20). Furthermore, the brute-force methodology of deep searches, which has worked so well in games such as chess, checkers and Othello, is not feasible due to the high branching ratio resulting from the probabilistic dice rolls. At each ply there are 21 dice combinations possible, with an average of about 20 legal moves per dice combination, resulting in a branching ratio of several hundred per ply. This is much larger than in checkers and chess (typical branching ratios quoted for these games are 8-10 for checkers and 30-40 for chess), and too large to reach significant depth even on the fastest available supercomputers.

In the absence of exact tables and deep searches, computer backgammon programs have to rely on heuristic postional judgment. The typical approach to this in backgammon and in other games has been to work closely with human experts, over a long period of time, to design a heuristic evaluation function that mimics as closely as possible the positional knowledge and judgment of the experts [1]. The supervised training approach of Neurogammon, described in the previous section, is another methodology that also relies on human expertise. In either case, building human expertise into an evaluation function, whether by knowledge engineering or by supervised training, has been found to be an extraordinarily difficult undertaking, fraught with many potential pitfalls. While there has been some success with these techniques, there has nevertheless remained a substantial gap between the positional judgment of the best humans and the ability of knowledge engineers or supervised learning programs to encapsulate that judgment in the form of a heuristic evaluation function.

A further problem is that the human expertise that is being emulated is not infallible. As human knowledge and understanding of a game increase, the concepts employed by experts and the weightings associated with those concepts undergo continual change. This has been especially true in Othello and in backgammon, where over the last 20 years, there has been a substantial revision in the way experts evaluate positions. Many strongly held beliefs of the past, that were held with near unanimity among experts, are now believed equally strongly to be erroneous. (Some examples of this will be discussed later.) In view of this, programmers are not exactly on firm ground in accepting current expert opinions at face value.

In the following section, we shall see that TD-Gammon represents a radically different approach toward developing a program capable of sophisticated positional judgment. Rather than trying to imitate humans, TD-Gammon develops its own sense of positional judgment by learning from experience in playing against itself. While it may seem that forgoing the tutelage of human masters places TD-Gammon at a disadvantage, it is also liberating in the sense that the program is not hindered by human biases or prejudices that may be erroneous or unreliable. Indeed, we shall see that the result of TD-Gammon's self-training process is an incredibly sophisticated evaluation function which, in at least some cases, appears to surpass the positional judgment of world-class human players.

We now present a brief summary of the TD backgammon learning system. For more details, the reader is referred to [15]. At the heart of TD-Gammon is a neural network, illustrated in Figure 1, that is organized in a standard multilayer perception (MLP) architecture. The MLP architecture, also used in the widely known backpropagation algorithm for supervised training [9] may be conveniently thought of as a generic nonlinear function approximator. Its output is computed by a feed-forward flow of activation from the input nodes to the output nodes, passing through one or more layers of internal nodes called "hidden" nodes. Each of the connections in the network is parameterized by a real valued "weight." Each of the nodes in the network outputs a real number equal to a weighted linear sum of inputs feeding into it, followed by a nonlinear sigmoidal "squashing" operation that maps the total summed input into the unit interval.

The nonlinearity of the squashing function enables the neural network to compute nonlinear functions of its input, and the precise function implemented depends on the values of the weights. In both theory and in practice, MLPs have been found to have extremely robust function approximation capabilities. In fact, theorists have proven that, given sufficient hidden units, the MLP architecture is capable of approximating any nonlinear function to arbitrary accuracy [5].

The process of "learning" in an MLP consists of applying a formula for changing the weights so that the function implemented by the network more closely approximates a desired target function. For large networks with thousands of connections, it is generally not feasible to find the globally optimal set of weights that gives the best possible approximation. Nevertheless, there are many reasonably efficient learning rules, such as backpropagation, that can find a locally optimal set of weight values. Such locally optimal solutions are often satisfactory for many classes of real-world applications.

The training procedure for TD-Gammon is as follows: the network observes a sequence of board positions starting at the opening position and ending in a terminal position characterized by one side having removed all its checkers. The board positions are fed as input vectors x[1], x[2], . . . , x[f] to the neural network, encoded using a representation scheme that is described later. (Each time step in the sequence corresponds to a move made by one side, i.e., a "ply" or a "half-move" in game-playing terminology.) For each input pattern x[t] there is a neural network output vector Y[t] indicating the neural network's estimate of expected outcome for pattern x[t]. (For this system, Y[t] is a four component vector corresponding to the four possible outcomes of either White or Black winning either a normal win or a gammon. Due to the extreme rarity of occurrence, triple-value backgammons were not represented.) At each time step, the TD(lambda) algorithm is applied to change the network's weights. The formula for the weight change is as follows:

where alpha is a small constant (commonly thought of as a "learning rate" parameter, w is the vector of weights that parameterizes the network, and is the gradient of network output with respect to weights. (Note that the equation expresses the weight change due to a single output unit. In cases where there are multiple output units, the total weight change is given by the sum of the weight changes due to each individual output unit.)

The quantity lambda is a heuristic parameter controlling the temporal credit assignment of how an error detected at a given time step feeds back to correct previous estimates. When lambda = 0, no feedback occurs beyond the current time step, while when lambda = 1, the error feeds back without decay arbitrarily far in time. Intermediate values of lambda provide a smooth way to interpolate between these two limiting cases.

At the end of each game, a final reward signal z (containing four components as described previously) is given, based on the outcome of the game. The preceding equation is used to change the weights, except that the difference (z - Y[f]) is used instead of (Y[t+1] - Y[t]).

In preliminary experiments, the input representation only encoded the raw board information (the number of White or Black checkers at each location), and did not utilize any additional pre-computed features relevant to good play, such as, e.g., the strength of a blockade or probability of being hit. These experiments were completely knowledge-free in that there was no initial knowledge built in about how to play good backgammon. In subsequent experiments, a set of handcrafted features (the same set used by Neurogammon) was added to the representation, resulting in higher overall performance.

During training, the neural network itself is used to select moves for both sides. At each time step during the course of a game, the neural network scores every possible legal move. (We interpret the network's score as an estimate of expected outcome, or "equity" of the position. This is a natural interpretation which is exact in cases where TD(lambda) has been proven to converge.) The move that is selected is then the move with maximum expected outcome for the side making the move. In other words, the neural network is learning from the results of playing against itself. This self-play training paradigm is used even at the start of learning, when the network's weights are random, and hence its initial strategy is a random strategy. Initially, this methodology would appear unlikely to produce any sensible learning, because random strategy is exceedingly bad, and because the games end up taking an incredibly long time: with random play on both sides, games often last several hundred or even several thousand time steps. In contrast, in normal human play games usually last on the order of 50-60 time steps.

The rather surprising finding was that a substantial amount of learning actually took place, even in the zero initial knowledge experiments utilizing a raw board encoding. During the first few thousand training games, these networks learned a number of elementary strategies and tactics, such as hitting the opponent, playing safe, and building new points. More sophisticated concepts emerged later, after several tens of thousands of training games. Perhaps the most encouraging finding was good scaling behavior, in the sense that as the size of the network and amount of training experience increased, substantial improvements in performance were observed. The best performance obtained in the raw-encoding experiments was for a network with 40 hidden units that was trained for a total of 200,000 games. This network achieved a strong intermediate level of play approximately equal to Neurogammon. An examination of the input-to-hidden weights in this network revealed interesting spatially organized patterns of positive and negative weights, roughly corresponding to what a knowledge engineer might call useful features for game play [15]. Thus the neural networks appeared to be capable of automatic "feature discovery," one of the longstanding goals of game learning research since the time of Samuel. This has been an extremely difficult problem for which substantial progress has only recently been made, for example, in [4].

Since TD-trained networks with a raw input encoding were able to achieve parity with Neurogammon, it was hoped that by adding Neurogammon's hand-designed features to the raw encoding, the TD nets might then be able to surpass Neurogammon. This was indeed found to be the case: the TD nets with the additional features, which form the basis of version 1.0 and subsequent versions of TD-Gammon, have greatly surpassed Neurogammon and all other previous computer programs. Among the indicators contributing to this assessment (for more details, see the appendix) are numerous tests of TD-Gammon in play against several world-class human grandmasters, including Bill Robertie and Paul Magriel, both noted authors and highly respected former World Champions.

Results of testing against humans are summarized in Table 1. In late 1991, version 1.0 played a total of 51 games against Robertie, Magriel, and Malcolm Davis, the 11th-highest rated player in the world at the time, and achieved a very respectable net loss of 13 points, for an average loss rate of about one-quarter point per game. Version 2.0 of the program, which had much greater training experience as well as a 2-ply search algorithm, made its public debut at the 1992 World Cup of Backgammon tournament. In 38 exhibition games against top human players such as Kent Goulding, Kit Woolsey, Wilcox Snellings, former World Cup Champion Joe Sylvester, and former World Champion Joe Russell, the program had a net loss of only 7 points. Finally, the latest version of the program (2.1) achieved near-parity to Bill Robertie in a recent 40-game test session. Robertie actually trailed the entire session, and only in the very last game was he able to pull ahead for an extremely narrow 1-point victory.

According to an article by Bill Robertie published in Inside Backgammon Magazine [8], TD-Gammon's level of play is significantly better than any previous computer program. Robertie estimates that TD-Gammon 1.0 would lose on average in the range of 0.2 to 0.25 points per game against world-class human play. (This is consistent with the results of the 51-game sample.) In human terms, this is equivalent to an advanced level of play that would have a decent chance of winning local and regional Open-division tournaments. In contrast, most commercial programs play at a weak intermediate level that loses well over one point per game against world-class humans. The best previous commercial program scored -0.66 points per game on this scale. The best previous program of any sort was probably Hans Berliner's BKG program. BKG, which was developed in the 1970s, was by far the strongest program of that era, and in its only public appearance in 1979 it won a short match against the World Champion at that time [1]. BKG was about equivalent to a very strong intermediate or weak advanced player, and Robertie estimates that it would have scored in the range of -0.3 to -0.4 points per game.

Based on the latest 40-game sample, Robertie's overall assessment is that TD-Gammon 2.1 now plays at a strong master level that is extremely close (within a few hundredths of a point) to equaling the world's best human players. In fact, due to the program's steadiness (it never gets tired or careless, as even the best of humans inevitably do), he thinks it would actually be the favorite against any human player in a long money game session or in a grueling tournament format such as the World Cup competition. The only real problems Robertie sees in the program's play are minor technical errors in its endgame play, and minor doubling cube errors. On the plus side, he thinks that in at least a few cases, the program has come up with some genuinely novel strategies that actually improve on the way top humans usually play.

In addition to Robertie's quite favorable assessment, an independent and even more favorable opinion has been offered by Kit Woolsey, who is one of the game's most respected analysts in addition to being perennially rated as one of the ten best players in the world. (He was rated fifth in the world in 1992 and currently holds the #3 spot.) Woolsey has performed a detailed analysis of dozens of the machine's games, including "computer rollout" analysis of all the difficult move decisions. As explained in the appendix, a rollout is a statistical method for quantitatively determining the best move, in which each candidate position is played to completion thousands of times, with different random dice sequences. Computer rollouts have been found to be remarkably trustworthy for many classes of positions, even if the program doing the rollout is only of intermediate strength.

As a result of Woolsey's extensive analysis, he now thinks that TD-Gammon's edge over humans in positional judgment holds in general and is not just limited to a few isolated cases. The following is an excerpt from his written evaluation (Woolsey, personal communication):

"TD-Gammon has definitely come into its own. There is no question in my mind that its positional judgment is far better than mine. Only on small technical areas can I claim a definite advantage over it . . . .
I find a comparison of TD-Gammon and the high-level chess computers fascinating. The chess computers are tremendous in tactical positions where variations can be calculated out. Their weakness is in vague positional games, where it is not obvious what is going on . . . . TD-Gammon is just the opposite. Its strength is in the vague positional battles where judgment, not calculation, is the key. There, it has a definite edge over humans. Its technique is less than perfect in such things as building up a board with no opposing contact, and bearing in against an anchor. In these sorts of positions the human can often come up with the better play by calculating it out . . . . In the more complex positions, TD has a definite edge. In particular, its judgment on bold vs. safe play decisions, which is what backgammon really is all about, is nothing short of phenomenal.
I believe this is true evidence that you have accomplished what you intended to achieve with the neural network approach. Instead of a dumb machine which can calculate things much faster than humans such as the chess playing computers, you have built a smart machine which learns from experience pretty much the same way humas do. It has the ability to play many more games than a human can play and correlate the results of its experiences much more accurately and with no emotional bias. Having done so, it can examine any position, add up all its parameters, and come up with a proper evaluation. Humans cannot do this with the same degree of perfection."

As one might expect from such favorable assessments, TD-Gammon has had a rather significant impact on the human expert backgammon community. TD-Gammon's style of play frequently differs from traditional human strategies, and in at least some cases, its approach appears to give better results. This has led in some cases to major revisions in the positional thinking of top human players. 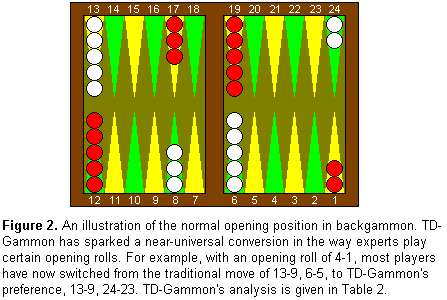One important area where this has occurred, illustrated in Figure 2 and Table 2, is in opening play. For example, with an opening roll of 2-1, 4-1, or 5-1, the near-universal choice of experts over the last 30 years has been to move a single checker from the 6 point to the 5 point. This technique, known as "slotting," boldly risks a high probability of being hit in exchange for the opportunity to quickly develop a menacing position if missed. However, when Bill Robertie's article on TD-Gammon appeared in Inside Backgammon in 1992, it included a rollout analysis by TD-Gammon showing that the opening slot was inferior to splitting the back checkers with 24-23. As a result, a few top players began experimenting with the split play, and after some notable tournament successes, it quickly gathered more adherents. Today, the near-universal choice is now the split play, whereas the slotting play has virtually disappeared from tournament competition.

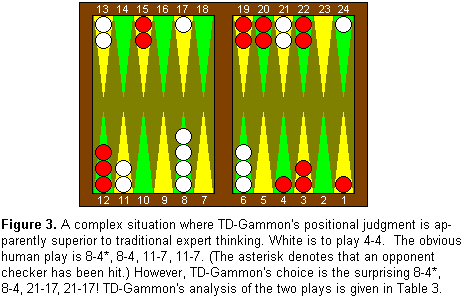
TD-Gammon's preference for splitting over slotting is just one simple example where its positional judgment differs from traditional expert judgment. A more complex and striking example is illustrated in Figure 3. This situation confronted Joe Sylvester, the highest-rated player in the world at the time, in the final match of the 1988 World Cup of Backgammon tournament. Sylvester, playing White, had rolled 4-4 and made the obvious-looking play of 8-4*, 8-4, 11-7, 11-7. His play was approved by three world-class commentators on the scene (Kent Goulding, Bill Robertie and Nack Ballard), and in fact it's hard to imagine a good human player doing anything else. However, TD-Gammon's recommendation is the surprising 8-4*, 8-4, 21-17, 21-17! Traditional human thinking would reject this play, because the 21 point would be viewed as a better defensive anchor than the 17 point, and the 7 point would be viewed as a better blocking point than the 11 point. However, an extensive rollout performed by TD-Gammon, summarized in Table 3, confirms that its choice offers substantial improvement in equity of nearly a tenth of a point. Since a TD-Gammon rollout is now generally regarded as the most reliable method available for analyzing checker plays, most experts are willing to accept that its play here must be correct. Results such as this are leading many experts to revise substantially their approach to evaluating complex positional battles. For example, it appears that in general, the 17 point is simply a much better advanced anchor than most people had realized.

If TD-Gammon has been an exciting new development in the world of backgammon, it has been even more exciting for the fields of neural networks and machine learning. By combining the TD approach to temporal credit assignment with the MLP architecture for nonlinear function approximation, rather surprising results have been obtained, to say the least. The TD self-play approach has greatly surpassed the alternative approach of supervised training on expert examples, and has achieved a level of play well beyond what one could have expected, based on prior theoretical and empirical work in reinforcement learning. Hence there is now considerable interest within the machine learning community in trying to extract the principles underlying the success of TD-Gammon's self-teaching process. This could form the basis for further theoretical progress in the understanding of TD methods, and it could also provide some indication as to other classes of applications where TD learning might also be successful. While a complete understanding of the learning process is still far away, some important insights have been obtained, and are described in more detail here.

In absolute terms, TD-Gammon's equity estimates are commonly off by a tenth of a point or more. At first glance, this would appear to be so large that the neural network ought to be essentially useless for move selection. Making master-level plays very often requires discrimination on a much finer scale than one-tenth of a point. Yet despite the large errors in TD-Gammon's evaluations, it is consistently able to make master-level move decisions. How is this possible?

The answer turns out to lie in the distinction between absolute error and relative error. When TD-Gammon makes a move decision, the errors made in evaluating each candidate play are not random, uncorrelated errors, but are in fact highly correlated. This correlation seems to come from similarity-based generalization of the neural network. In making a move decision, one has to choose between several candidate positions that are all very similar-looking. This is because they are all reached by small changes from a common starting position. Since the candidate positions have such a high degree of similarity, the neural network's equity estimates will all be off by approximately the same amount of absolute error. Thus the potentially large absolute errors effectively cancel when comparing two candidate plays, leaving them ranked in the proper order.

A second key ingredient is the stochastic nature of the task coming from the random dice rolls. One important effect of the stochastic dice rolls is that they produce a degree of variability in the positions seen during training. As a result, the learner explores more of the state space than it would in the absence of such a stochastic noise source, and a possible consequence could be the discovery of new strategies and improved evaluations. In contrast, in deterministic games a system training by self-play could end up exploring only some very narrow portion of the state space, and might develop some horrible strategy that nevertheless gives self-consistent results when implemented against itself over the narrow range of positions that it produces. Pathologies due to self-play training have in fact been found in the deterministic games of checkers [10] and Go [11] and a good general discussion is given in [2].

Another effect of random dice is that they contribute to the terminal states of the system being attractors (i.e., for all playing strategies including random strategies, the sequences of moves will eventually terminate in either a won or lost state). In backgammon this comes about partly due to the dice rolls, and partly due to the fact that one can only move one's pieces in the forward direction. The only way checkers ever move backwards is when they are hit by the opponent. These two factors imply that, even for random initial networks, games usually terminate in, at most, several thousand moves. On the other hand, in deterministic games it is possible that a random initial strategy might execute simple cycles that would last forever (unless the rules prohibited such cycles). In such cases the network could not learn, as it would never receive the final reward signal; special techniques would be required to prevent this from happening.

Finally, non-deterministic games have the advantage that the target function one is trying to learn, the true expected outcome of a position given perfect play on both sides, is a real-valued function with a great deal of smoothness and continuity, that is, small changes in the position produce small changes in the probability of winning. In contrast, the true game-theoretic value function for deterministic games like chess is discrete (win, lose, draw) and presumably more discontinuous and harder to learn.

A third key ingredient has been found by a close examination of the early phases of the learning process. As stated previously, during the first few thousand training games, the network learns a number of elementary concepts, such as bearing off as many checkers as possible, hitting the opponent, playing safe (i.e., not leaving exposed blots that can be hit by the opponent) and building new points. It turns out that these early elementary concepts can all be expressed by an evaluation function that is linear in the raw input variables. Thus what appears to be happening in the TD learning process is that the neural network first extracts the linear component of the evaluation function, while nonlinear concepts emerge later in learning. (This is also frequently seen in backpropagation: in many applications, when training a multilayer net on a complex task, the network first extracts the linearly separable part of the problem.)

In particular, when the input variables encode the raw board information such as blots and points at particular locations, a linear function of those variables would express simple concepts such as "blots are bad" and "points are good." Such concepts are said to be context-insensitive, in that the evaluation function assigns a constant value to a particular feature, regardless of the context of the other features. For example, a constant value would be assigned to owning the 7 point, independent of the configuration of the rest of the board. On the other hand, an example of a context-sensitive concept that emerges later in learning is the notion that the value of the 7 point depends on where one's other checkers are located. Early in the game, when one has several checkers to be brought home, the 7 point is valuable as a blocking point and as a landing spot. On the other hand, if one is bearing in and all other checkers have been brought home, the 7 point then becomes a liability.

It turns out that the linear function learned early on by the TD net gives a surprisingly strong strategy -- it is enormously better than the random initial strategy, and in fact is better than typical human beginner-level play. As such it may provide a useful starting point for subsequent further learning of nonlinear, context-sensitive concepts.

Temporal difference learning appears to be a promising general-purpose technique for learning with delayed rewards. The technique can be applied both to prediction learning, and as shown in this work, to a combined prediction/control task in which control decisions are made by optimizing predicted outcome. Based on the surprising quality of results obtained in the backgammon application, it now appears that TD methods may be much more powerful than previously suspected. As a result there is substantial interest in applying the TD methodology in other problem domains, as well as in improving the existing theoretical understanding of TD, particularly in the general nonlinear case.

Despite the very strong level of play of TD-Gammon, there are nevertheless ample opportunities for further improvement of the program. As with any game-playing program, one can try to obtain greater performance by extending the search to greater depth. The current version of the program is able to execute a heuristic 2-ply search in real time. If this could be extended to 3-ply, it appears that many of the program's technical endgame errors would be eliminated. In fact, a 3-ply analysis is commonly employed by authors of backgammon texts and annotated matches to explain how to find the best move in certain kinds of endgame situations. One could also try to design some handcrafted feature detectors that deal specifically with these situations, and provide them as additional inputs to the neural network. One might also expect that further scaling of the system, by adding more hidden nodes and increasing the amount of training experience, would continue to yield further improvements in playing ability.

Beyond these obvious suggestions, a potentially wide-open topic for further investigation involves modifications of the learning methodology used here. The experiments done in this work have only scratched the surface of possible learning methodologies. Any number of modifications to the existing system can be considered; here are a few such ideas: (a) A dynamic schedule could be used to vary the lambda parameter during training. Intuitively it makes sense to begin training with a large value of lambda and then decrease it as the learning progresses. (b) Variations on the greedy self-play training paradigm (i.e., the network plays against itself and it always makes the move it thinks is best) may be considered. Other alternatives are training by playing against experts and training by playing through recorded expert games. One intriguing suggestion which has been effective with the game-learning system HOYLE is called "lesson-and-practice" training, in which short sessions of training against experts are interspersed with longer sessions of self-play practice sessions [2]. (c) Other function approximation architectures besides the multilayer perception might prove to be useful. Furthermore, dynamically growing the architecture during training, as is done in the Cascade-Correlation procedure [3], avoids the problem of having to restart training from random initial control whenever the size of the network is increased.

It is interesting to speculate on the implications of TD-Gammon's results for other potential applications of TD learning, both within the field of computer games and in other fields. TD-Gammon represents a radically different approach to equaling and possibly exceeding human preformance in a complex game. Instead of using massive computing power for deep on-line searches, TD-Gammon uses massive computing power for extensive off-line training of a sophisticated evaluation function. Such an approach could provide an interesting complement to current work on high-level programs in chess and related games.

A number of researchers are currently investigating applications of TD(lambda) to other games such as chess and Go. Sebastian Thrun has obtained encouraging preliminary results with a TD-chess learning system that learns by playing against a publicly available chess program, Gnuchess (Thrun, personal communication). Schraudolph, et al. have also obtained encouraging early results using TD(lambda) to learn to play Go [11]. Finally, Jean-Francois Isabelle has obtained good results applying the TD self-learning procedure to Othello [6]. The best network reported in that study was able to defeat convincingly an "intermediate-advanced" conventional Othello program.

In more complex games such as chess and Go, one would guess that an ability to learn a linear function of the raw board variables would be less useful than in backgammon. In those games, the value of a particular piece at a particular board location is more dependent on its relation to other pieces on the board. A linear evaluation function based on the raw board variables might not give very good play at all -- it could be substantially worse than beginner-level play. In the absence of a suitable recoding of the raw board information, this might provide an important limitation in such cases to the success of a TD learning system similar to the one studied here.

It would also seem that TD approaches to deterministic games would require some sort of external noise source to produce the variability and exploration obtained from the random dice rolls in backgammon. There are many conceivable methods of adding such noise -- one could randomize the initial positions at the start of every training game, or one could have the network choose moves according to some probability distribution. Noise injection was found to be important in the work of [6, 11].

Finally, there are also a number of potential applications of TD learning outside the domain of games, for example, in areas such as robot motor control and financial trading strategies. For these sorts of applications, one may lose the important advantage one has in games of being able to simulate the entire environment. In learning to play a game, it is not necessary to deal with the physical constraints of a real board and pieces, as it is much easier and faster to simulate them. Furthermore, the "action" of the learning agent is just a selection of which state to move to next, from the list of legal moves. It is not necessary to learn a potentially complex "forward model" mapping control actions to states. Finally, within the simulated environment, it is possible to generate on-line a potentially unlimited amount of training experience, whereas in, for example, a financial market one might be limited to a fixed amount of historical data. Such factors imply that the best way to make progress initially would be to study applications where most or all of the environment can be effectively simulated, e.g., in certain robotic navigation and path planning tasks, in which the complexity lies in planning the path, rather than in mapping the motor commands to resulting motion in physical space.

There are a number of methods available to assess the quality of play of a backgammon program; each of these methods has different strengths and weaknesses. One method is automated play against a benchmark computer opponent. If the two programs can be interfaced directly to each other, and if the programs play quickly enough, then many thousands of games can be played and accurate statistics can be obtained as to how often each side wins. A higher score against the benchmark opponent can be interpreted as an overall stronger level of play. While this method is accurate for computer programs, it is hard to translate into human terms.

A second method is game play against human masters. One can get an idea of the program's strength from both the outcome statistics of the games, and from the masters' play-by-play analysis of the computer's decisions. The main problem with this method is that game play against humans is much slower, and usually only a few dozen games can be played. Also the expert's assessment is at least partly subjective, and may not be 100% accurate.

A third method of analysis, which is new but rapidly becoming the standard among human experts, is to analyze individual move decisions via computer rollouts. In other words, to check whether a player made the right move in a given situation, one sets up each candidate position and has a computer play out the position to completion several thousand times with different random dice sequences. The best play is assumed to be the one that produced the best outcome statistics in the rollout. Other plays giving lower equities are judged to be errors, and the seriousness of the error can be judged quantitatively by the measured loss of equity in the rollout.

In theory, there is a potential concern that the computer rollout results might not be accurate, since the program plays imperfectly. However, this apparently is not a major concern in practice. Over the last few years, many people have done extensive rollout work with a commercial program called "Expert Backgammon," a program that does not actually play at expert level but nevertheless seems to give reliable rollout results most of the time. The consensus of expert opinion is that, in most "normal" positions without too much contact, the rollout statistics of intermediate-level computer programs can be trusted for the analysis of move decisions. (They are less reliable, however, for analyzing doubling decisions.) Since TD-Gammon is such a strong program, experts are willing to trust its results virtually all the time, for both move decisions and doubling decisions. While computer rollouts are very compute-intensive (usually requiring several CPU hours to analyze one move decision), they provide a quantitative and unbiased way of measuring how well a human or computer played in a given situation.

The author thanks Steve White and Jeff Kephart for helpful comments on an earlier version of the manuscript.

1. Berliner, H. Computer backgammon. Sci. Amer. 243, 1, (1980), 64-72.
2. Epstein, S. Towards an ideal trainer. Mach. Learning 15, 3, (1994), 251-277.
3. Fahlman, S. E. and Lebiere, C. The cascade-correlation learning architecture. In D. S. Touretzky, Ed. Advances in Neural Information Processing Systems 2, Morgan Kaufmann, San Mateo, Calif., (1990), 524-532.
4. Fawcett, T. E. and Utgoff, P. E. Automatic feature generation for problem solving systems. In D. Sleeman and P. Edwards Eds., Machine Learning: Proceedings of the Ninth International Workshop, Morgan Kaufman, San Mateo, Calif., 1992, 144-153.
5. Hornik, K., Stinchcombe, M. and White, H. Multilayer feedforward networks are universal approximators. Neural Networks 2, (1989), 359-366.
6. Isabell, J.-F. Auto-apprentissage, à l'aide de réseaux de neurones, de fonctions heuristiques utilisées dans les jeux stratégiques. Master's thesis, Univ. of Montreal, 1993.
7. Magriel, P. Backgammon. Times Books, New York, 1976.
8. Robertie, B. Carbon versus silicon: Matching wits with TD-Gammon. Inside Backgammon 2, 2, (1992), 14-22.
9. Rumelhart, D. E., Hinton, G. E. and Williams, R. J. Learning internal representation by error propagation. In D. Rumelhart and J. McClelland, Eds., Parallel Distributed Processing, Vol. 1. MIT Press, Cambridge, Mass., 1986.
10. Samuel, A. Some studies in machine learning using the game of checkers. IBM J. of Research and Development 3, (1959), 210-229.
11. Schraudolph, N. N., Dayan, P. and Sejnowski, T. J. Temporal difference learning of position evaluation in the game of Go. In J. D. Cowan, et al. Eds., Advances in Neural Information Processing Systems 6, 817-824. Morgan Kaufmann, San Mateo, Calif., 1994.
12. Shannon, C. E. Programming a computer for playing chess. Philosophical Mag. 41, (1950), 265-275.
13. Sutton, R. S. Learning to predict by the methods of temporal differences. Mach. Learning 3, (1988), 9-44.
14. Tesauro, G. Neurogammon wins Computer Olympiad. Neural Computation 1, (1989), 321-323.
15. Tesauro, G. Practical issues in temporal difference learning. Mach. Learning 8, (1992), 257-277.
16. Zadeh, N. and Kobliska, G. On optimal doubling in backgammon. Manage. Sci. 23, (1977), 853-858.

GERALD TESAURO is a research staff member at IBM. Current research interests include reinforcement learning in the nervous system, and applications of neural networks to financial time-series analysis and to computer virus recognition. Author's Present Address: IBM Thomas J. Watson Research Center, P.O. Box 704, Yorktown Heights, NY, 10598; email: tesauro@watson.ibm.com